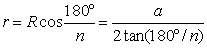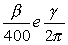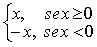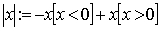Matematica Dizionario a b c d e f g i k l m n o p q r s t u v z
Dizionario di matematica e geometria iniziale A
ACUTO, ANGOLO
Un angolo acuto è un angolo di ampiezza inferiore a quella di un angolo retto.
ADDIZIONE
L'addizione è una delle operazioni fondamentali dell'aritmetica. Nella sua forma più semplice, l'addizione combina due numeri (termini), gli addendi, in un singolo numero, la somma. Aggiungere altri numeri corrisponde a un'addizione ripetuta. Per estensione, è possibile definire l'addizione di zero, uno o infiniti numeri.Definizione dell'operazione di addizione
Proprietà importanti
Se si somma un numero finito di numeri, non importa come vengono raggruppati (proprietà associativa della somma) o in che ordine vengono sommati (proprietà commutativa della somma): si ottiene sempre lo stesso risultato.Se si somma zero a un numero qualsiasi, il risultato è il numero di partenza: zero è l'elemento neutro per l'addizione.
La somma di un numero e del suo opposto (ammesso che esso esista: ad esempio nell'insieme dei numeri naturali non esiste l'opposto) è zero. Pertanto,se la somma è 1+(-1), il risultato sarà sempre 0.
Notazione
Se i suoi termini sono scritti individualmente, allora l'addizione si scrive con il segno più ("+"). La somma di 1, 2 e 4 si indica pertanto come 1 + 2 + 4 = 7.Se i termini non sono scritti individualmente, la somma si può indicare con un'ellissi ("...") per indicare i termini mancanti: la somma dei numeri naturali da 1 a 100 si può dunque scrivere come 1 + 2 + ... + 99 + 100 = 5050.
In alternativa, la somma può essere rappresentata con il simbolo di sommatoria, che è una lettera greca Sigma maiuscola. La definizione tecnica è la seguente:
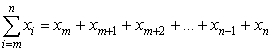
Il pedice è il simbolo per una variabile dummy, i. Qui, i rappresenta l'indice della sommatoria; m è il limite inferiore della sommatoria, e n il limite superiore della sommatoria. Ad esempio:
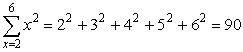
È anche possibile considerare somme di un numero infinito di termini; esse sono chiamate serie infinite. Come notazione, al posto dell'n sopra il simbolo di sommatoria si usa il simbolo di infinito (∞).
La somma di una serie siffatta è definita come il limite della somma dei primi n termini, al crescere di n oltre un qualsivoglia valore. In formule,
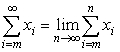
Si può anche rimpiazzare m con un infinito negativo, e avere
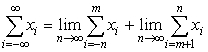
per un intero a scelta m, ammesso che entrambi i limiti esistano.
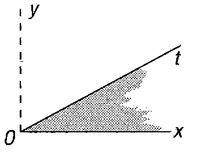
Si hanno spesso generalizzazioni di questa notazione, in cui viene posta una condizione logica arbitraria, e la somma si intende essere su tutti i valori che soddisfano tale condizione. Per esempio,
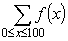
è la somma di f(x) su tutti gli (interi) x nell'intervallo specificato,
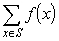
è la somma su tutti gli x appartenenti all'insieme S, e
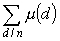
è la somma di μ(d) su tutti gli interi d che dividono n.
Relazioni con le altre operazioni e le costanti
È possibile sommare meno di due numeri:- si definisce la somma di un singolo termine x come x.
- si definisce la somma di zero termini come zero, perché zero è l'elemento identità per l'addizione. In questo caso si parla anche di somma vuota.
Ci sono molte altre operazioni che si possono vedere come somme generalizzate. Se un singolo termine x appare in una somma n volte, allora la somma è nx, il risultato di una moltiplicazione. Dato che anche se n non è un numero naturale la moltiplicazione può avere senso, si può dare una definizione di sommare un termine "per due volte e mezzo".
Un caso speciale della moltiplicazione come somma ripetuta è dato dalla moltiplicazione per -1, che porta al concetto di inverso additivo, e alla sottrazione, l'operazione inversa dell'addizione.
La versione più generale di queste idee è la combinazione lineare, dove un numero qualunque di termini viene incluso nella somma generalizzata per un numero qualunque di volte.
ADIACENTE
Rende conto, per due figure, di una certa forma di prossimità, e si dice in particolare di angoli e di segmenti.Due angoli si dicono adiacenti quando hanno in comune un lato, il vertice (e null'altro), mentre gli altri lati sono semirette opposte.
Due segmenti si dicono adiacenti quando sono contenuti nella stessa retta, e hanno in comune un estremo, e nessun altro punto.
In un poligono, si parla di lato adiacente a un angolo quando il primo è anche un lato del secondo.
Due vertici si dicono adiacenti quando sono collegati da uno spigolo.
ALGEBRA
Il termine algebra deriva dall'arabo "al-djebr" che significa "unione", "connessione" o "completamento" (ma anche "aggiustare"). Essa è una branca della matematica e può essere definita come generalizzazione ed estensione dell'aritmetica. L'algebra si basa sull'applicazione di operatori matematici a delle espressioni matematiche. Si basa sul principio che se un operazione viene eseguita da un lato di un equazione la medesima operazione deve essere eseguita anche dell'altro lato.Nell'algebra viene molto utilizzata la legge distributiva per isolare i termini incogniti e per risolverli.
Il campo dell'algebra si divide sommariamente in:
- algebra elementare - che studia le operazioni sui numeri reali o loro sottoinsiemi e le equazioni polinomiali con le loro soluzioni.
- algebra astratta - che studia al livello generale e formale strutture algebriche come: semigruppi, gruppi, anelli, campi, reticoli, moduli, spazi vettoriali, algebre, bialgebre.
Consente la formulazione generale di leggi aritmetiche (come a + b = b + a per ogni a e b), e quindi è il primo passo per un'esplorazione sistematica delle proprietà del sistema dei numeri reali.
Consente di riferirsi a numeri "sconosciuti" e quindi di formulare delle equazioni e di sviluppare tecniche per risolverle (per esempio: "trova un numero x tale che
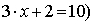
Consente la formulazione di relazioni funzionali (come la seguente: "se si
vendono x biglietti, allora il profitto sarà 10x - 5 euro")
Questi sono problemi tipicamente nell'ambito dell'algebra elementare, che si
distingue dall'algebra astratta, un argomento molto più avanzato e affrontato
generalmente negli studi universitari.
Nell'algebra, una espressione può contenere numeri, variabili ed operazioni aritmetiche; esempi sono a + 3 e x2 - 3. Un'equazione è l'affermazione che due espressioni siano uguali. Alcune equazioni sono vere per ogni valore delle variabili incognite (per esempio a + (b + c) = (a + b) + c); esse sono conosciute come identità. Altre equazioni contengono dei simboli per le variabili incognite e siamo quindi interessati a trovare quei valori che rendono vera l'equazione: x2 - 1 = 4. Essi sono le soluzioni dell'equazione.
Come nell'aritmetica, anche nell'algebra è importante sapere come debbano essere interpretate le espressioni matematiche. Ciò è stabilito dalle regole dell'ordine delle operazioni.
È necessario essere in grado di semplificare le espressioni algebriche. Per esempio, l'espressione
- 4(2a + 3) - a
può essere scritta nella forma equivalente
- 9a - 12.
Le equazioni più semplici da risolvere sono quelle lineari, come
2x + 3 = 10
La tecnica fondamentale è quella di aggiungere, sottrarre, moltiplicare o dividere entrambi i membri di un'equazione per lo stesso numero, e, ripetendo più volte questo processo, arrivare ad esprimere direttamente il valore della x. Nell'esempio precedente, se noi sottraiamo 3 da entrambi i membri, otteniamo
2x = 7
e dividendo entrambi i membri per 2, otteniamo la soluzione
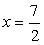
Equazioni come
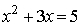
sono note come equazioni quadratiche e si risolvono con una formula risolutiva.
Espressioni o affermazioni possono contenere molte variabili, da cui potrebbe essere possibile o impossibile ricavare il valore di alcune variabili. Per esempio:
(x - 1)2 = 0y
Dopo alcuni semplici passaggi algebrici, possiamo dedurre che x = 1, ma non possiamo dedurre quale sia il valore di y. Comunque, se noi avessimo avuto un'altra equazione delle incognite x e y, avremmo potuto ottenere la risposta tramite un sistema di equazioni. Per esempio:
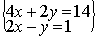
Ora, moltiplichiamo la seconda per 2, ottenendo le seguenti espressioni:
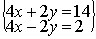
Poiché abbiamo moltiplicato l'intera equazione per due (ossia entrambi i membri), abbiamo in realtà ottenuto un'affermazione equivalente. Ora possiamo combinare le due equazioni, sommando membro a membro:
8x = 16
In questo modo abbiamo ottenuto una equazione in una sola incognita, che possiamo facilmente risolvere dividendo per 8 e ottenendo x = 2.
4x + 2y = 14
Sostituiamo 2 al posto di x.
4(2) + 2y = 14
Semplifichiamo
8 + 2y = 14
2y = 6
E risolviamo per y, ottenendo 3. La soluzione di questo problema è x = 2 e y = 3, ossia la coppia (2, 3).
ALGEBRICI, NUMERI
In matematica, un numero algebrico è un numero reale o complesso che è soluzione di un'equazione polinomiale della forma:anxn + an−1xn−1 + ··· + a1x + a0 = 0
dove n > 0, ogni ai è un intero, e an è diverso da 0.
Tutti i numeri razionali sono algebrici perché ogni frazione a / b è soluzione di bx − a = 0.
Anche alcuni numeri irrazionali come 21/2 (la radice quadrata di 2) e 31/3/2 (la radice cubica di 3 divisa per 2)
sono algebrici perché radici, rispettivamente, di x2 − 2 = 0 and 8x3 − 3 = 0.
Ma non tutti i numeri reali sono algebrici.
Esempi di π e e.
Se un numero reale (o complesso) non è un numero algebrico, viene chiamato numero trascendente. Se un numero algebrico soddisfa un'equazione come quella data sopra con un polinomio di grado n e nessuna equazione di grado inferiore, allora si dice che il numero è un numero algebrico di grado n.
Le operazioni di somma, differenza, prodotto e quoziente di due numeri algebrici generano ancora numeri algebrici, pertanto essi formano formano un campo. Si può dimostrare che se ammettiamo che i coefficienti ai siano numeri algebrici qualsiasi, allora ogni soluzione dell'equazione sarà ancora un numero algebrico. Ciò può essere espresso in altre parole dicendo che il campo dei numeri algebrici è algebricamente chiuso.
ALLINEATI
Punti allineati sono punti che stanno su una stessa retta. La proprietà di più punti di essere allineati si dice proprietà di allineamento.
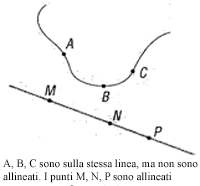
Questa proprietà " comincia " dunque con tre punti, perché per due punti passa sempre una e una sola retta. Tre punti presi a casa nel piano non hanno alcuna ragione per essere allineati, e pertanto, quando lo sono, ciò può accadere:
- o perché lo si è voluto all'inizio, cioè questa disposizione è dunque specificata fin da principio;
- o perché si tratta di una proprietà, in generale notevole, della figura ottenuta ed è allora il caso di dimostrare tale proprietà.
ALTERNI ESTERNI, ALTERNI INTERNI
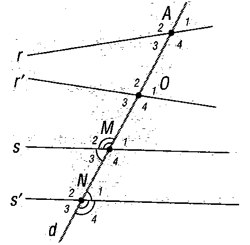
Espressione matematica che descrive le posizioni degli angoli determinati da due rette e da una secante: infatti, alterni è un termine tecnico della geometria che significa "disposto su due lati diversi".Nella figura, la retta d incontra sia r e r', sia s e s' (queste ultime rette parallele). In entrambi i casi si dicono alterni due angoli che si trovano da parti opposte di d, e precisamente esterni se sono all'esterno della regione compresa fra r e r' (o s e s'), interni se sono all'interno.
Numeriamo gli angoli di vertice A, O, M, N e
designamo per esempio con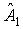 
l'angolo di vertice A numerato 1:
- Sono alterni esterni:
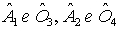se si considerano r e r';- gli angoli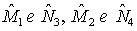 
se si considerano s e
s';
- Sono alterni interni:
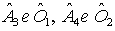se si considerano r e r';- gli angoli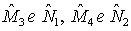 
se si considerano s e
s'.
Nella geometria euclidea, una proprietà caratteristica di due rette parallele è che due angoli alterni interni hanno la stessa ampiezza (analogamente per due angoli alterni esterni).
ALTEZZA
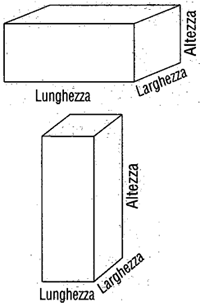
In geometria una delle tre dimensioni dello spazio ordinario, rappresentate dalla lunghezza, dalla larghezza e dall'altezza di un parallelepipedo.
Ma, mentre per tali oggetti supposti sistemati su un piano orizzontale queste dimensioni sono intercambiabili " la lunghezza può diventare altezza ", questo non succede per altri solidi quali un cilindro, un cono, una piramide o un generico prisma per i quali la posizione della base " o di una delle basi ", se si tratta di un oggetto materiale, è imposta dalla sua forma, dalle nostre abitudini o convenzioni nell'appoggiarlo e, dunque, nel vederlo.
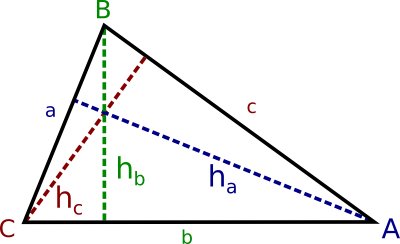
Altezze di un triangolo
L'altezza di un triangolo è il segmento perpendicolare alla base che ha per estremi il vertice opposto alla base e un punto della base stessa. Ogni triangolo possiede quindi tre altezze ognuna delle quali è associata ad un lato.In base al tipo di triangolo le altezze possono essere tutte uguali (triangolo equilatero, nel qual caso le altezze coincidono con le bisettrici e le mediane), possono esserci due altezze uguali (triangolo isoscele); negli altri casi le altezze sono tutte diverse.
Proprietà delle altezze dei triangoli
Le tre altezze di un triangolo sono incidenti in un punto detto ortocentro del triangolo.Il triangolo ottenuto congiungendo i piedi delle altezze si dice traingolo ortico del triangolo ABC.
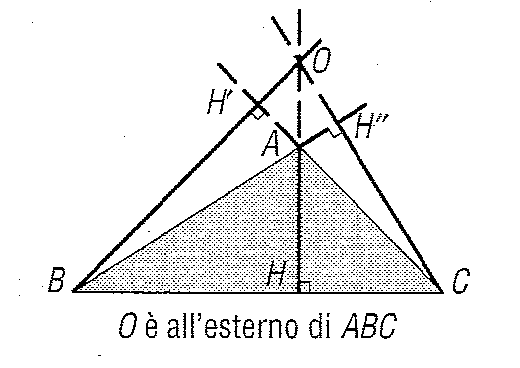
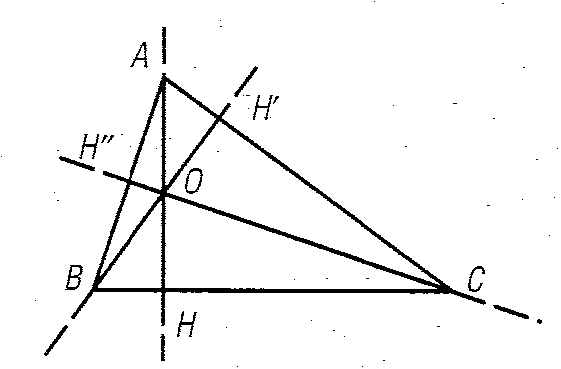
Se un triangolo è ottusangolo " cioè se uno dei suoi angoli è ottuso " due delle sue altezze cadono all'esterno del triangolo, sul prolungamento del lato opposto
Se un triangolo è rettangolo, due delle sue altezze coincidono con i lati dell'angolo retto. Ecco perché nel caso di un triangolo rettangolo si parla in genere di altezza riferendosi all'altezza relativa all'ipotenusa.
L'ortocentro di un triangolo può essere pertanto situato:
- all'interno del triangolo: è il caso dei triangoli acutangoli;
- all'esterno del triangolo: è il caso dei triangoli ottusangoli;
- su un vertice del triangolo: è il caso dei triangoli rettangoli, il cui ortocentro coincide con il vertice dell'angolo retto.
ANGOLO
Un angolo è ciascuna delle due parti di un piano delimitata da due semirette, dette lati, aventi in comune il loro punto origine, detto vertice dell'angolo. Si dice concavo se contiene i prolungamenti dei lati, convesso se non li contiene.
L'angolo può essere anche descritto in termini cinematici come la superficie
coperta da una semiretta durante una rotazione planare attorno alla sua origine.
Gli angoli vengono indicati di solito con le lettere greche minuscole.
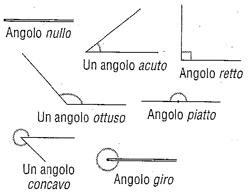
Angoli particolari
- Un angolo associato al movimento di una semiretta che compie un'intera rotazione attorno alla sua origine vertice, fino a tornare nella posizione originaria, si dice angolo giro. All'angolo giro si assegna una misura, la sua ampiezza, di 360 gradi, ovvero di 2π radianti.
- Un angolo che corrisponde a mezza rotazione di una semiretta attorno al vertice, arrivando a formare con la semiretta iniziale una intera retta, si dice angolo piano o angolo piatto. L'angolo piatto ha ampiezza di 180 gradi, ovvero di π radianti, ovvero la metà dell'angolo giro. Nella geometria euclidea la somma degli angoli interni di un triangolo è pari ad un angolo piatto.
- Un angolo che corrisponde a un quarto di rotazione attorno al vertice si
dice
angolo retto. L'angolo retto ha ampiezza di 90 gradi, ovvero di
π/2 radianti; esso è
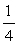dell'angolo giro. Una definizione immediata, intuitiva e corretta dell'angolo
retto: se da un punto di una retta si alza una semiretta a formare due angoli
uguali, allora si hanno due angoli retti. - L'angolo acuto è un angolo la cui ampiezza misura meno di 90 gradi, ovvero è minore di un angolo retto.
- L'angolo ottuso è un angolo maggiore di 90 gradi, ovvero maggiore dell'angolo retto.
- Due angoli si dicono complementari se la loro somma è un angolo retto.
- Si dicono invece supplementari se la loro somma è un angolo piatto.
- Infine si dicono esplementari se la loro somma è un angolo giro.
- Due angoli si dicono opposti al vertice se i prolungamenti di uno corrispondono ai lati dell'altro, cioè semirette opposte. Due angoli opposti al vertice sono congruenti.
- Due angoli sono consecutivi se hanno in comune un vertice e un lato.
- Due angoli sono adiacenti se sono consecutivi e i lati non comuni sono semirette opposte.
La misura dell'angolo
Fin dall'antichità è in uso il sistema dei gradi. Con lo sviluppo dell'analisi infinitesimale è stata introdotta una unità di misura che per certi scopi risulta più naturale chiamata radiante, in cui l'angolo piatto ha misura π. Nell'uso quotidiano il grado è preferito per la maggiore semplicità dei calcoli. L'argomento può essere approfondito introducendo lo studio delle funzioni circolari.
Somma degli angoli interni
Nella geometria euclidea la somma degli angoli interni di un triangolo è sempre di 180 gradi. Più in generale, data una qualunque figura geometrica convessa di n lati, la somma di tutti i suoi angoli interni è uguale a (n − 2) · 180 gradi. Quindi, per esempio, la somma totale di tutti gli angoli interni di un quadrilatero è uguale a (4 − 2) · 180 = 2 · 180 = 360 gradi. Un caso particolare è dato dal quadrato, che ha quattro angoli retti, la cui somma è infatti 360 gradi. Analogamente, la somma di tutti gli angoli interni di un pentagono, regolare o meno, è uguale a 540 gradi.In altre geometrie, dette geometrie non euclidee, la somma degli angoli interni di un triangolo può assumere sia valori maggiori che minori di 180 gradi.
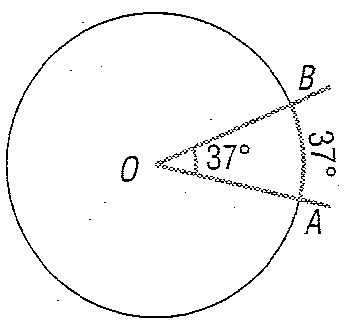
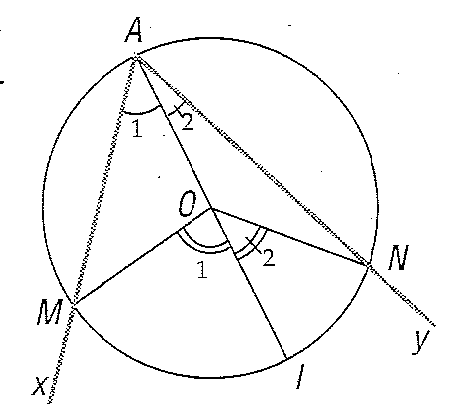
Angolo al centro
Un angolo al centro ha la stessa misura dell'arco intercettato.
Si parla così tanto di un arco di 37° quanto di un angolo di 37°, perché, rapportando il piano alla circonferenza di centro O divisa in 360 parti, i 37/360 della circonferenza (l'arco) corrispondono ai 37/360 del piano (l'angolo).
Angolo alla circonferenza
Data una circonferenza C, un agolo alla circonferenza è un angolo (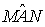
)
il cui vertice sta su C. Si dice che esso insiste sull'arco di estremi
M, N, al quale non appartiene il vertice A.
Dato l'angolo alla circonferenza, ci si può chiedere che relazione c'è con
l'angolo al centro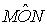 
.
Mentre la misura di questo è la stessa dell'arco, si dimostra facilmente che
l'ampiezza dell'angolo 
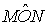è
doppia di quella dell'angolo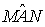 
.
Infatti, basta condurre il diametro AI. L'ampiezza di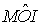 
,
angolo esterno al triangolo isoscele AOM, è doppia di quella di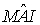 
;
analogamente per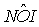 
e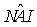 
.
Sommando, si trova che l'ampiezza di
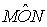è doppia di quella di 
.
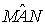Pertanto: l'angolo al centro ha ampiezza doppia dell'angolo alla circonferenza che insiste sullo stesso arco.
APOTEMA
In geometria il termine apotema viene usato in corrispondenza di alcune figure geometriche tendenzialmente regolari per denotare uno o più segmenti congruenti che le caratterizzano o, più spesso, la loro lunghezza.Apotema di un poligono regolare
Segmento che parte dal centro del poligono e cade perpendicolarmente su un suo lato, ovvero la loro lunghezza comune. Tale lunghezza individua il raggio del cerchio inscritto nel poligono. Nel caso di poligono regolare di n lati ciascuno di lunghezza a, con raggio del cerchio circoscritto uguale ad R, l'apotema r è data da
Apotema di una piramide
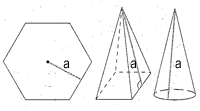
Retta con base regolare è ogni segmento che cade dall'apice della piramide perpendicolarmente su un suo lato di base, cioè ogni segmento che congiunge il suo apice al punto medio di ogni suo lato di base, ovvero la loro lunghezza comune.Apotema di un cono retto
Ogni segmento che congiunge il suo apice a un punto della circonferenza di base, ovvero la sua lunghezza, cioè la lunghezza dell'ipotenusa del triangolo rettangolo con il quale si può definire il cono stesso.Si osserva che quest'ultima definizione si può considerare un caso limite della precedente. La definizione di apotema di un poligono regolare si può estendere in modo prevedibile ai poliedri che hanno facce poligonali congruenti come i solidi platonici.
APPROSSIMATO, VALORE
Nel calcolo decimale, si è costretti a dare a quei numeri che non si possono scrivere in forma decimale (finita) dei valori approssimati. Per esempio, si utilizza per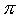
,
fin dall'infanzia, un valore approssimato, 3,14, e a volte, per maggior precisione, 3,1416. È dunque ben chiaro che prendendo 3,14 o 3,1416 in luogo di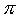 
,
si utilizzano dei valori che non sono uguali a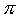 
,
ma ai quali questo è vicino: sono approssimazioni di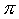 
.A scuola si propongono due modi per approssimare un numero. Qui parleremo di numeri assoluti.
a. Il modo più semplice è la
troncatura: si lasciano cadere i decimali che non si vogliono. Per esempio, 3,14 o 3,141, o 3,1415, o 3,14159 ecc. sono valori approssimati di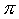 
troncati rispettivamente alla seconda, terza, quarta e quinta cifra dopo la virgola; questi numeri sono dunque tutti minori del "vero" valore di 
,
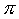e si chiameranno approssimazioni per difetto.
b. Il metodo di approssimazione più logico è invece l'arrotondamento:
poiché c'è in ogni modo uno scarto fra il valore "vero" e quello che si assume, si può fare in modo che questo scarto sia il minimo possibile scegliendo
caso per caso un valore approssimato di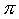 
che gli sia inferiore (dunque approssimato per difetto), oppure superiore (dunque approssimato per eccesso).
ARCO
In geometria si definisce arco la parte di una curva regolare compresa fra due suoi punti, detti estremi dell'arco. Curve regolari sono le curve continue e dotate di tangente unica in ogni punto. Un arco può essere approssimato da una linea spezzata poligonale con segmenti sufficientemente piccoli inscritta nell'arco stesso. Quando la lunghezza dei segmenti tende a zero, la lunghezza della poligonale tende a quella dell'arco. Il segmento di retta delimitato dagli estremi di un arco si dice corda sottesa dall'arco.Arco di circonferenza: figura e grandezza
Un arco di circonferenza è una figura, cioè un insieme di punti; poiché si tratta di una linea, un arco di circonferenza ha una lunghezza, ma non è una lunghezza.Le misure degli archi di circonferenza sono espresse frequentemente in gradi sessagesimali, centesimali o radianti, assumendo la circonferenza stessa, ovvero parte di essa, come unità di misura.Se
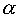è la misura in gradi sessagesimali di un arco, questo è 
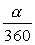della sua circonferenza. Se 
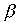è la misura in gradi centesimali, e 
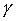la sua misura in radianti, la stessa parte di circonferenza si esprime con
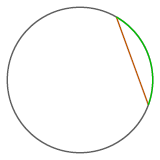
(In verde, un arco di circonferenza; in rosso, la corda sottesa)
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
AREA
L'area è una misura dell'estensione di una regione bidimensionale di uno spazio, ovvero la misura di una superficie. Come per le altre misure di natura geometrica, per la precisione si dovrebbe distinguere fra la regione bidimensionale (insieme di punti) e la sua area (valore numerico associato alla precedente). Spesso però, nel parlare comune ma anche in esposizioni scientifiche, il termine area e il termine superficie vengono usati intercambiabilmente.Aree di figure piane
- L'area di un quadrato è il prodotto del lato per se stesso:
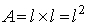. - L'area di un rettangolo è il prodotto della base per l'altezza:
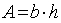(dove b è la lunghezza della base e h l'altezza). - L'area di un cerchio è il prodotto del raggio al quadrato per la costante
matematica
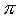(che si ottiene dal rapporto tra la circonferenza e il diametro di un cerchio): 
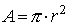. - L'area di un ellisse è il prodotto dei due semiassi per la costante
matematica
: 
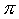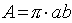. - L'area di un poligono regolare è il prodotto del perimetro per l'apotema
(ovvero la distanza tra il centro ed un lato) diviso 2:
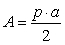. - L'area di un trapezio è il prodotto della somma della base maggiore con la
base minore per l'altezza diviso 2:
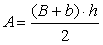(dove B e b sono le lunghezze delle basi ed h l'altezza). - L'area di un triangolo è il prodotto della base per l'altezza diviso 2:
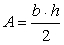(dove b è la lunghezza della base e h l'altezza corrispondente). - L'area sottesa da una funzione f(x) è pari all'integrale definito della
funzione stessa
.
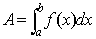Aree delle superfici di figure tridimensionali
- L'area di un cubo è il prodotto del lato al quadrato per le 6 facce del
cubo:
,
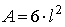dove l è la lunghezza del lato - L'area di una sfera è il prodotto che si ottiene moltiplicando 4 volte il
raggio al quadrato per la costante matematica
:
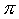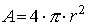
- L'area di un cilindro è il prodotto che si ottiene moltiplicando 2 volte il
raggio per la costante matematica
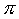per la somma del raggio di base più l'altezza: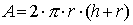 
Unità di misura per le aree
Sono state e sono tuttora utilizzate numerose unità di misura dell'area. Nel passato si sceglievano unità sulla base di esigenze locali e, in particolare nel mondo rurale, si avevano misure diverse anche in regioni limitrofe. Successivamente, a partire dalle spinte illuministiche, si sono date definizioni razionali e unificanti. Qui presentiamo le unità più importanti.- metro quadrato (m2, o mq) - è l'unità del Sistema Internazionale
- centimetro quadrato (cm2), 1 cm2 = 0,0001 m2 - è l'unità del sistema cgs
- ara: 1 ara = 100 m2 (usata per misurare l'estensione di terreni)
- ettaro: 1 ettaro = 10.000 = m2 (usata per misurare l'estensione di terreni)
- chilometro quadrato: 1 km2 = 1.000.000 m2 (usato per la misura di territori di estensione media e grande (superfici comunali, provinciali, regionali, nazionali, continentali e planetarie)
- piede quadrato: 1 piede quadrato = 0,09290304 m2 - (unità di misura anglosassone)
- iarda quadrata: 1 iarda quadrata = 9 piedi quadrati = 0,83612736 m2
- miglio quadrato: 1 miglio quadrato = 2.589.988,1103 m2
- acro internazionale: 1 acro = 4.046,8564 m2
ARITMETICA
L'aritmetica è un ramo della matematica che studia le proprietà elementari di certe operazioni sui numeri, specialmente i numeri interi.Operazioni aritmetiche
Le operazioni aritmetiche tradizionali sono addizione, sottrazione, moltiplicazione e divisione, sebbene vengano a volte incluse nella materia anche operazioni più avanzate come l'elevamento a potenza, l'estrazione di radice, i logaritmi e l'uso delle percentuali. I calcoli aritmetici vengono effettuati rispettando l'ordine delle operazioni.Teoria dei numeri
Il termine aritmetica è usato anche per riferirsi alla teoria dei numeri. Quest'ultima studia le proprietà degli interi collegate ai numeri primi, la divisibilità, e le soluzioni intere delle equazioni, che sono argomenti in rapida crescita nella matematica moderna. È in questo contesto che si incontrano il teorema fondamentale dell'aritmetica e le funzioni aritmetiche.ASCISSA
In matematica si può introdurre il piano cartesiano come piano della geometria euclidea munito di due rette ortogonali su ciascuna delle quali si fissa un orientamento (rette orientate) e per le quali si fissa una unica unità di misura che consente di esprimere i loro punti mediante numeri reali. Il punto nel quale le due rette si incontrano viene detto origine.Tra le due
rette si distingue una prima chiamata asse delle ascisse o
asse delle x e una seconda detta asse delle ordinate o asse
delle y. Il sistema costituito dalla coppia dei due assi (e implicitamente
dall'origine) si dice sistema di riferimento cartesiano ortogonale del
piano. Esso consente di individuare ogni punto del piano con una coppia di
numeri reali chiamati rispettivamente ascissa e ordinata del
punto; le coordinate di un punto generico del piano o di un punto che si pensa
variabile spesso si denotano con x e y. Talora il sistema dei due
assi si denota con Oxy. Un generico punto si può quindi esprimere
scrivendo (x,y) oppure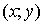 
.
Dato su una retta r un sistema di riferimento (di origine O e punto unità I), l'ascissa di un punto M è il numero che serve a individuarlo. Essa è il rapporto fra la lunghezza del segmento OM e quella del segmento OI: lo si considera positivo se M sta dalla setssa parte di I rispetto a O, altrimenti lo si considera negativo.
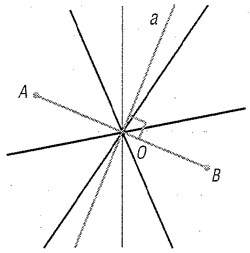
ASSE
In matematica possiamo dire genericamente che il termine asse viene usato in diversi contesti per indicare una linea retta con un ruolo particolare. Es: l' asse sono quei punti equidistanti da i due estremi di un segmento.Asse di un segmento
Sia dato un segmento AB. Fra tutte le rette che passano per il punto medio O di AB, ce n'è una sola che sia perpendicolare a tale segmento; tale retta è l'asse del segmento AB.
L'asse di un segmento è l'insieme dei punti equidistanti dagli estremi del segmento.
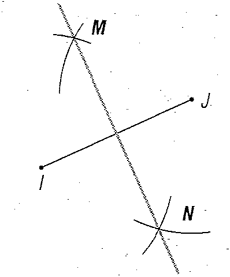
Sia dato un segmento IJ; prendendo come centri I e J, si tracciano da una parte e dall'altra di IJ due archi di circonferenza con lo stesso raggio che si tagliano nei punti M e N: essendo M e N equidistanti da I e da J, la retta MN è l'asse cercato.
In geometria l'asse è una retta attorno alla quale una figura solida compie un moto rotatorio, o che definisce la riflessione di una figura piana. In quest'ultimo caso la retta prende il nome di asse di simmetria.
L'asse di un triangolo è la retta perpendicolare a un lato che parte dal suo punto medio. L'incrocio degli assi definisce il circocentro.
Con asse di riferimento intendiamo una retta orientata facente parte di un sistema di riferimento cartesiano; a tali assi fanno riferimento i grafici delle funzioni di variabili reali o complesse.
ASSOLUTO, VALORE
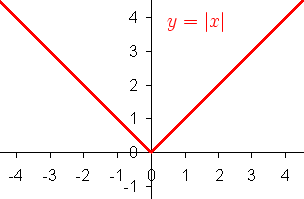
In matematica, il valore assoluto (o modulo) di un numero reale è il suo valore numerico a meno del segno. Quindi, ad esempio, 3 è il valore assoluto sia di 3 che di -3, mentre 0 è l'unico valore assoluto di 0. Dato un numero x il suo valore assoluto si rappresenta con |x|. Il valore assoluto di un numero non è mai minore di zero. Il valore assoluto di un numero reale r minore di zero è -r, cioè si ottiene ponendo il segno negativo davanti al numero.
[Grafico della funzione valore assoluto]
Valore assoluto di un numero reale
Nel caso di numeri reali il valore assoluto è cosi definito:|x| :=
Equivalentemente mediante le pratiche parentesi di Iverson si definisce
Il valore assoluto può essere considerato come la distanza di un numero dallo zero.
Proprietà
Il valore assoluto ha le seguenti proprietà:- |a| ≥ 0
- |a| = 0 se (se e solo se) a = 0.
- |ab| = |a||b|
- |a/b| = |a| / |b| (con b ≠ 0)
- |a+b| ≤ |a| + |b| (la disuguaglianza triangolare)
- |a−b| ≥ ||a| − |b||
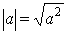
- |a| ≤ b sse −b ≤ a ≤ b
- |a| ≥ b sse a ≤ −b or b ≤ a
|x − 3| ≤ 9
−9 ≤ x−3 ≤ 9
−6 ≤ x ≤ 12
Numeri complessi
Nel caso di un numero complesso c il valore assoluto è definito come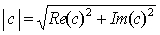
dove Re(c) è la parte reale del numero e Im(c) la parte immaginaria.
In maniera equivalente si può definire il modulo di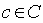 
come 
,
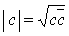dove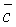 
è il complesso coniugato di c.
Questa definizione di valore assoluto su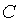 
soddisfa le proprietà dalla 1 alla 6 sopra indicate.
Funzione modulo
Per argomenti reali, la funzione valore assoluto f(x) = |x| è continua ovunque e derivabile per x ≠ 0. La funzione non è invertibile, in quanto lo stesso valore assoluto è condiviso da un numero negativo e da uno positivo (tranne che nel caso dello zero).Per argomenti complessi, la funzione è sempre continua ma non è mai differenziabile.
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
